L'Offerta economicamente più vantaggiosa (OPEV) e il confronto a coppie con il metodo AHP

Le linee guida dell’ANAC n. 2/2016, di attuazione del D. Lgs. 18/04/2016 n. 50 hanno lo scopo di dare precise indicazioni operative per il calcolo dell’offerta economicamente più vantaggiosa, in relazione ai criteri di attribuzione dei punteggi per i diversi elementi qualitativi e quantitativi che compongono l’offerta e la successiva applicazione dei punteggi ivi calcolati. Al capitolo V di tali linee guida, sono espressamente indicati i metodi per la valutazione degli elementi qualitativi, che qui testualmente si riportano. Per determinare il criterio di attribuzione dei punteggi, per i criteri di natura qualitativa, si ricorre abitualmente a due tipologie di sistemi:

1. L’attribuzione discrezionale di un coefficiente variabile da zero a uno, da parte di ciascun commissario di gara;
2. Il confronto a coppie fra le offerte presentate, sempre da parte di ciascun commissario di gara. All’interno della seconda modalità, sono presenti il metodo del confronto a coppie e l’utilizzo della metodologia basata sul calcolo dell’autovettore principale della matrice completa dei confronti a coppie. Nella pratica operativa, però, questo ultimo metodo risulta ancora poco utilizzato, anche se lo stesso, potendo valutare la qualità dei punteggi, è di gran lunga preferibile; qui tratteremo del suo impiego e delle possibilità applicative dello stesso nella valutazione dei criteri di natura qualitativa per la scelta delle offerte migliori in gare di appalto.

Storia e genesi del metodo AHP

Il metodo AHP (Analytic Hierarchy Process) fu introdotto dal matematico iracheno naturalizzato statunitense Thomas L. Saaty all’inizio degli anni Settanta e precisamente nel 1971, quando Saaty, all’epoca dirigente di progetti di ricerca alla Disarmament Agency, presso il U.S. Department of State, riscontrando la difficoltà di comunicazione tra i vari membri partecipanti ai singoli progetti, pensò ad un sistema per scomporre ed analizzare i vari problemi da affrontare e giungere ad una decisione condivisa. La piena completezza del metodo arrivò dopo ulteriori due anni di studi e prove, ossia nel 1973. La metodologia sarà poi affinata dal punto di vista teorico negli anni successivi per giungere a definitivo compimento verso il 1980.

Inizialmente impiegato per lo studio dei piani di azione per la crescita economica dei paesi sottosviluppati dell’Africa, fu poi impiegato per risolvere problemi decisionali in molteplici settori, fra i quali l’economia, l’assistenza sanitaria e l’educazione.

Oggi costituisce un metodo largamente applicato nel campo delle metodologie decisionali multicriterio ed è ampiamente utilizzato nel campo dell’analisi costibenefici, in scelte finalizzate ad investimenti economici in ogni settore di attività, nella valutazione di nuove alternative e soluzioni tecnologiche e nel campo della pianificazione strategica. Fra i vari testi e pubblicazioni riguardanti tale metodologia è d’obbligo segnalare il testo scritto da Saaty nel 1980 ed intitolato “The Analytic Hierarchy Process”, considerato unanimemente il più importante e completo su questo argomento.

Basi scientifiche del metodo AHP

L’ AHP è uno dei metodi di analisi multicriterio che permette di stabilire delle priorità ad una serie di alternative decisionali.

Si parla di alternativa decisionale quando ci sono più possibilità di intraprendere una scelta per raggiungere un obbiettivo.

Il processo decisionale, chiamato anche decision making, usualmente prevede i seguenti passi fondamentali:

1. Individuazione dei possibili scenari alternativi fra loro;
2. Valutazione degli stessi e delle loro conseguenze future;
3. La scelta finale dell’opzione migliore.

Una modalità di raffronto per la scelta delle opzioni migliori è quella di confrontare in maniera totalmente indipendente i giudizi sui singoli componenti, e fra i metodi usualmente utilizzabili per operare tale confronto, uno particolarmente impiegato è quello del confronto a coppie fra le varie opzioni.

Tuttavia tale metodologia, presenta un inconveniente, che è quello di creare inconsistenza, ossia non perfetta corrispondenza e transitività fra i giudizi assunti.

Per specificare meglio cosa intendiamo per inconsistenza, facciamo un semplice esempio pratico. Se abbiamo tre alternative possibili, che chiameremo per semplicità Alfa, Beta e Gamma, possiamo stabilire un ordine in cui Alfa è migliore di Beta e Beta è migliore di Gamma. Se anche Alfa è migliore di Gamma diciamo che il problema della scelta in questione, è perfettamente consistente, altrimenti si crea inconsistenza, ossia non c’è coerenza di scelta.

Nel metodo del confronto a coppie, si possono creare dei giudizi inconsistenti, ossia si può definire Alfa migliore di Beta e Beta migliore di Gamma, ma questo non implica che Alfa sia migliore di Gamma, ossia si potrebbe avere un giudizio in cui viceversa Gamma è migliore di Alfa, generando inconsistenza.

Il metodo AHP fu introdotto, sostanzialmente, per verificare e stabilire se i giudizi espressi col metodo del confronto a coppie fossero consistenti o meno.

Saaty, osservando il metodo del confronto a coppie impiegato per risolvere conflitti decisionali e studiando più nel dettaglio il problema, osservò che lo stesso può essere sintetizzato come una matrice triangolare alta, come nella sottostante figura 1.

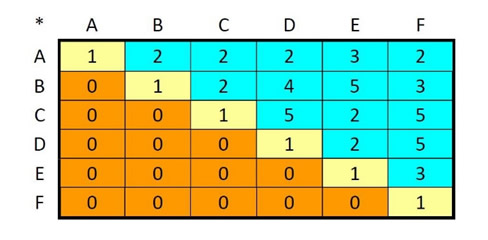
Figura 1: Matrice triangolare alta

Nella figura 1 possiamo vedere i confronti a coppie nelle celle evidenziate di celeste, mentre in quelle evidenziate di giallo abbiamo i confronti di ogni criterio con sé stesso (in questo caso indicati con 1) e nelle celle evidenziate di arancione si possono considerare i valori zero tipici di una matrice triangolare alta e completanti il confronto a coppie che definiremo “semplice” o “classico”.

Saaty provò così a riallacciarsi ad alcune caratteristiche generali delle matrici per poter fornire la soluzione al problema di verificare la consistenza dei giudizi espresso; osservando, in particolare, la seguente tipologia di matrici, che vengono definite consistenti, reciproche e simmetriche se valgono le relazioni di:

1. Reciprocità, se l’elemento a_J J della matrice è uguale a 1 : a_j j ;
2. Transitività, se a_j j = a_j k x a_k j,

Saaty riuscì così a trovare la chiave di volta per risolvere il problema, come vedremo nel prosieguo. Consideriamo adesso il seguente caso per meglio comprendere il significato delle proprietà appena osservate:

se il giudizio G₁ = 5G₂ e il giudizio G₁ = 9G₃ la matrice è detta consistente se 5G₂ = 9G₃

ossia quando

G₂ = (9/5)G₃,

dove con G_n si indicano le valutazioni o giudizi.

Nella figura 2 è riportata l’espressione matriciale

del caso considerato come si presenta in un foglio di calcolo elettronico. In blu sono evidenziati gli eventuali giudizi di un confronto a coppie ed in arancione gli elementi corrispondenti che completano la matrice con le proprietà viste sopra.

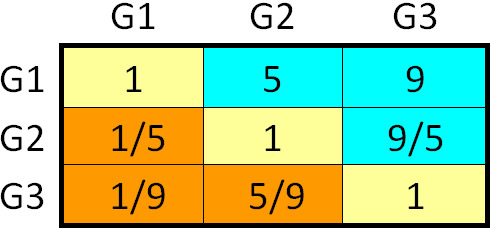
Figura 2: Matrice perfettamente consistente

Risultando soddisfatte le suddette condizioni, la matrice è detta perfettamente consistente.

Passiamo quindi ad esaminare i motivi per cui tali matrici possono essere scientemente utilizzate per verificare la consistenza dei giudizi in esame, nell’ambito appunto dell’aggiudicazione di gare pubbliche con il criterio del miglior rapporto qualità prezzo (già offerta economicamente più vantaggiosa).

Consideriamo una matrice perfettamente consistente, ossia una matrice gode delle proprietà di reciprocità e transitività, ed i cui elementi ai j sono uguali al rapporto v_i /v_j , dove v_i e v_j sono detti pesi, per i motivi che saranno chiariti successivamente.

La matrice considerata è, per semplicità computazionale, del tipo 3x3 e sarà indicata con la lettera A ed ogni elemento della stessa ai j è uguale al rapporto v_i / v_j , come si rileva dalla Figura 3

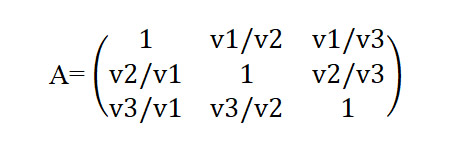
Moltiplicando detta matrice per il vettore V e ℜⁿ con

Figura 3: Matrice 3x3

Da quest’ultima equazione si evince che gli autovalori di questi tipi di matrice valgono n (in questo caso 3) e 0 ripetuto n1 volte, in questo caso 2, poiché una matrice di questo tipo per ogni ordine ha tutte le righe proporzionali, e rango sempre pari a uno. Tutti i suoi autovalori relativi sono inoltre nulli, eccetto l’autovalore principale uguale a n, e conseguentemente, tale matrice ha un’unica soluzione non nulla, a cui corrisponde l’autovettore V che ha per componenti i valori v_i che rappresentano così i pesi degli elementi posti a confronto, ossia la loro importanza.

In questo modo, generalizzando, si può utilizzare questa equazione per trovare l’autovettore corrispondente che sarà composto da soli elementi positivi, il quale, successivamente normalizzato, fornirà i corrispondenti valori delle sue componenti, che vengono definiti pesi; pesi utili per meglio evidenziare l’importanza specifica dei singoli elementi messi a confronto, come si può facilmente evincere dall’esempio soprastante, grazie alla parametrizzazione all’unità attraverso la normalizzazione.

Con questo ragionamento, inoltre, l’autovalore principale diviene così lo strumento per verificare la consistenza della matrice, ossia, nel caso di una matrice i cui elementi della porzione triangolare superiore sono i confronti a coppie e quelli della porzione triangolare inferiore soddisfano le proprietà elencate sopra, la validità dei giudizi espressi dal decisore. (Ricordiamo che si definiscono elementi della porzione triangolare superiore quelli posti sopra la diagonale principale della matrice).

Infatti la coerenza dei giudizi diventa verificabile mediante il calcolo dell’autovalore principale che indicheremo con λ_max definendo, come fatto da Saaty, l’indice di consistenza (CI) – consistency index:

CI = (λmax – n) / (n1)

Avendo la matrice sopra costruita λ_max = n, da questa relazione si evince facilmente che la matrice quando è consistente avrà CI=0, viceversa, in ogni altra situazione, deviando λ_max da n, la matrice non sarà perfettamente consistente e la relazione espressa dal confronto a coppie presenterà un grado di inconsistenza.

Disponendo di una matrice A, che diventa quella dei confronti a coppie, si possono utilizzare le deduzioni matematiche precedenti per valutarne la consistenza, pur sapendo che dai confronti stessi, risulteranno delle inconsistenze per cui l’equazione AV=nV non sarà soddisfatta come nell’esempio so prariportato e che CI sarà diverso da zero.

In generale, pertanto, le valutazioni eseguite non sono mai perfettamente consistenti e tale coefficiente, tipico delle matrici costruite con le proprietà di cui sopra, diventa così un indice prezioso per valutare la bontà delle scelte.

La metodologia AHP suggerita da Saaty segue questa filosofia e ammette un grado di inconsistenza, il cui valore limite è espresso da un valore numerico, tale che, se il risultato ottenuto è inferiore a tale valore limite, è considerato valido. Se però l’inconsistenza è superiore a tale valore, allora occorre rivedere i propri giudizi e/o la gerarchia del problema affrontato. Fra le cause di errore potrebbero risultare anche errori grossolani di inserimento dati, o una scelta errata del modello di valutazione.

Per valutare se i giudizi sono consistenti o meno, il metodo AHP implica pertanto il confronto dell’indice di consistenza con un valore detto Random Index (RI) ottenuto sperimentalmente dalla media degli indici di consistenza di un alto campione di matrici.

Secondo la teoria di Saaty se CI ≤ 0,1RI allora la matrice ed i relativi confronti si considerano accettabili. Quando il valore di CI supera una soglia pari al 10% di RI la deviazione dalla condizione di consistenza è ritenuta inaccettabile e pertanto i giudizi dovranno essere rivisti per aumentarne la coerenza e rientrare nel range di ammissibilità.

Il Random Index (RI) è la media dei valori di indici di consistenza, calcolati da un gruppo di specialisti, valutati in relazione ad un numero elevato di matrici quadrate, reciproche, positive e casuali ed i cui valori, dipendenti dall’ordine della matrice, si riportano nella sottostante tabella.

Ai fini pratici, tuttavia, per comodità, si calcola il rapporto di consistenza CR (Consistency Ratio): CR=CI/RI. Tale rapporto per avere consistenza dovrà essere inferiore a 0,1.

La valutazione di quest’ultimo numero fornisce lo strumento, quello che definiremo trigger, per valutare la transitività e l’efficienza dei giudizi espressi nella valutazione considerata in oggetto, come vedremo negli esempi seguenti.

Ai fini pratici, tuttavia, per comodità, si calcola il rapporto di consistenza CR (Consistency Ratio): CR=CI/RI. Tale rapporto per avere consistenza dovrà essere inferiore a 0,1

La valutazione di quest’ultimo numero fornisce lo strumento, quello che definiremo trigger, per valutare la transitività e l’efficienza dei giudizi espressi nella valutazione considerata in oggetto, come vedremo negli esempi seguenti.

Il Metodo AHP e la scala fondamentale di espressione dei giudizi

Secondo quanto argomentato nei paragrafi precedenti, da queste basi nasce il metodo AHP di Saaty, dove l’acronimo AHP ha il seguente significato:

• “A” sta per “analytic”: il metodo è analitico, in quanto si scompone un problema complesso nei suoi fattori costitutivi;
• “H” sta per “hierarchy”: il metodo prevede che esista un rapporto gerarchico di dominanza, ossia un albero al cui vertice è collocato l’obiettivo principale e da cui, disposti in livelli successivi, si dispongono i criteri ed i sotto criteri;
• “P” sta per process: il metodo consiste in un procedimento con il quale, attraverso una serie di operazioni, trasformazioni e modulazioni si arriva ad un risultato di tipo decisionale.

Dal punto di vista prettamente scientifico, sintetizzando, il metodo prevede due passaggi fondamentali:

• il primo passaggio che consiste nello scomporre il problema da affrontare in sotto problemi gerarchicamente connessi fra loro.
• il secondo passaggio che consiste nell’affrontare i vari sottoproblemi specifici con una serie di confronti a coppie fra le diverse opportunità di scelta, attribuendo a ciascun confronto un punteggio di importanza relativa, per concludersi, con l’assegnazione di un peso unitario o percentuale. La somma di tutti i pesi percentuali sarà pari ad uno o al 100%, a seconda della scala, assoluta o percentuale, utilizzata.

I punteggi usati per eseguire ogni confronto a coppie sono scelti da una scala di valutazione chiamata scala di Saaty, che utilizza una scala numerica, o linguistica, composta da 5 giudizi fondamentali e 4 intermedi; scala che qui riassumiamo come da tabella sottostante.

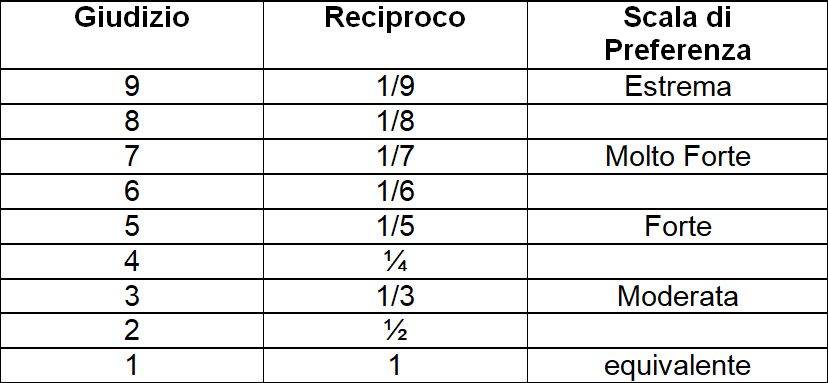
I valori di giudizio che hanno numero pari, sono valori di preferenza intermedia fra i valori dispari in cui sono ricompresi.

Vediamo una interpretazione dei giudizi per mezzo di un’altra tabella.

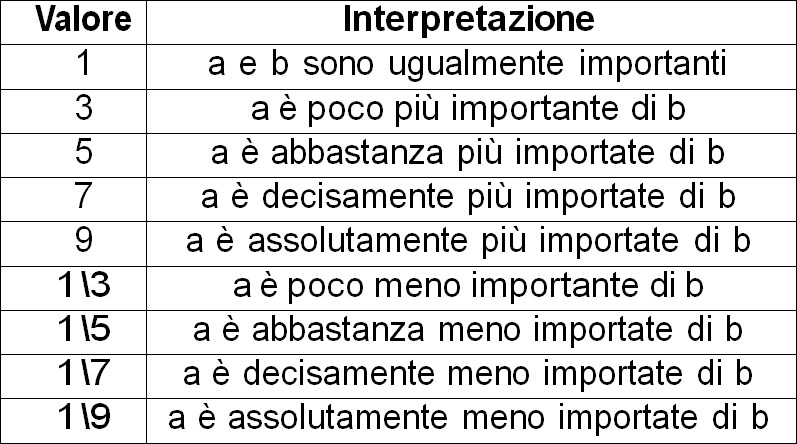
Saaty ideò tali scale, dette anche Scale Fondamentali, nel 1972.

Egli si basò sull’assunto, dimostrato, che gli esseri umani, classificano meglio gli elementi o fattori, in base ad un intervallo compreso da 1 a 9, e dopo aver verificato che questo era il miglior modo per valutare gli aspetti dei problemi decisionali messi a confronto.

Pertanto Saaty concluse che le scale così costruite permettono di valutare nella maniera più efficace informazioni di tipo quali-quantitativo e da allora i confronti eseguiti con questo metodo adottano questa metrica per la valutazione dei punteggi da dare ai giudizi espressi.

Il numero totale dei confronti a coppie da effettuare dipende dal numero di elementi da confrontare ed è pari a: n(n-1)/2, dove “n” è il numero di elementi da confrontare. Ad esempio se ci sono 3 giudizi avremo 3(3-1)/2 ossia 3 confronti, con n=6, si otterranno 6(6-1)/2 = 15 confronti.

Per applicare concretamente il metodo AHP, si deve costruire una matrice quadrata e considerarne la porzione triangolare alta. Sulla diagonale principale della matrice avremo sempre il valore 1, poiché ogni singolo elemento confrontato con sé stesso produce parità e quindi è espresso con valore unitario secondo la scala di Saaty.

Se l’elemento della colonna è preferito rispetto a quello della riga, si inserisce il valore reciproco, ossia si considera l’elemento della riga meno importante di quello della colonna; nel caso in cui l’elemento della riga sia preferito a quello della colonna, si inserisce il numero intero assoluto della scala di Saaty corrispondente al grado di preferenza scelto.

Dopo si procede a riempire la porzione triangolare bassa della matrice, inserendo nelle caselle rappresentanti gli elementi della matrice, i valori inversi corrispondenti degli elementi della porzione triangolare alta degli stessi.

La matrice che abbiamo visto inizialmente dal punto di vista teorico e che qui riportiamo:

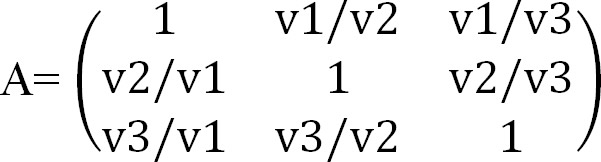
nel caso di inserimento in un foglio di calcolo elettronico, applicando le regole sovraesposte, conduce alla rappresentazione della figura 4.

I criteri o i concorrenti da valutare sono indicati con le lettere maiuscole. In giallo sono evidenziati gli elementi della diagonale principale, in marrone chiaro gli elementi da inserire nella porzione triangolare alta della matrice, come nel confronto a coppie usuale.

La porzione triangolare bassa della matrice sarà invece formata dai valori reciproci degli elementi ajj della parte triangolare alta della stessa, risultando così uguali a 1/a_jj come da teoria, ed evidenziati dalle celle in color arancione.

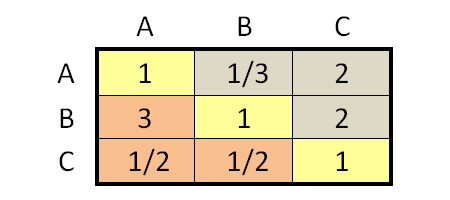
Figura 4: Matrice

Metodi approssimati

Il metodo matematico rigoroso, sopraesposto, richiede il calcolo di autovalori ed autovettori di matrici che possono avere ordini elevati, risultando così estremamente complicato da risolvere, a meno di disporre di programmi specialistici del tipo di Matlab, Maple o Wolfram Mathematica, i quali, oltre a comportare elevati costi di acquisto, richiedono anche una conoscenza d’uso specifica.

In alternativa si può ricorrere a metodi numerici, ma sono anch’essi laboriosi dal punto di vista computazionale, fra cui qui ricordiamo quello più usato, ossia il metodo Francis.

Si preferisce quindi ricorrere a metodi approssimati atti ad ottenere risultati di precisione accettabile, rispetto ai metodi canonici, computazionalmente più complicati e laboriosi.

Esistono molteplici metodi, ma descriveremo il metodo comunemente più usato ed un altro metodo approssimato impiegato usualmente nella valutazione degli elementi qualitativi degli appalti pubblici.

Nel metodo approssimato più utilizzato, per prima cosa viene normalizzata la matrice, sommando le colonne di questa e dividendo tutti gli elementi della matrice per la somma della colonna in cui si trovano. Dopodiché si calcola l’autovettore approssimato sommando i valori delle righe e dividendoli per il numero delle colonne, computando così ogni sua singola componente.

Un altro metodo utilizzato e che sarà poi quello impiegato per la successiva applicazione del metodo AHP nell’applicazione per la valutazione degli elementi qualitativi negli appalti pubblici, consiste nel moltiplicare gli elementi di ogni riga della matrice iniziale, nell’estrarne la radice n-esima del risultato ottenuto, dove “n” è il rango della matrice, per poi normalizzare i valori così derivati attraverso la divisione per il totale della somma di tutte le componenti dell’autovettore prima ricavato, al fine di calcolare l’autovettore normalizzato. In entrambi i casi, l’autovalore principale viene calcolato moltiplicando ogni elemento dell’autovettore normalizzato per il reciproco del numero risultante dalla somma delle componenti dell’autovettore non normalizzato e per la somma delle colonne della matrice non normalizzata. I valori risultanti vengono infine sommati fra loro per dare λ_max. Si vedano degli esempi di questo secondo metodo nelle pagine successive.

La consistenza è valutata usando sempre l’indice di consistenza e la procedura di calcolo del rapporto di consistenza CR così come nel metodo canonico.

Software utilizzabili

Il metodo AHP può essere implementato in fogli di calcolo come Excel, oppure può essere utilizzato attraverso l’uso di software altamente specializzati, fra i quali quello più comune e conosciuto è “Expert Choice”, un software commerciale a pagamento.

Sul portale Youtube, digitando Expert Choice, si possono trovare guide dedicate a tale software, che mostrano come utilizzarlo e le relative potenzialità.

Una risorsa disponibile gratuitamente si può trovare in internet presso il sito:

https://bpmsg.com/academic/ahp_calc.php

Il programma Excel o similari in ambito open-source, permettono di realizzare tabelle, grafici e gestire i dati in modo flessibile dall’utente che può adattarli al caso proprio e con la propria creatività, per renderli più comprensibili ad utenti esterni e funzionalizzarli alle singole esigenze.

Pertanto tale metodologia può essere sviluppata in un foglio di calcolo elettronico adattandola al caso in esame a discrezione dell’utilizzatore.

Metodo AHP e valutazione degli elementi qualitativi delle offerte tecniche

Nel caso della valutazione degli elementi qualitativi negli appalti pubblici, le linee guida dell’ANAC n. 2/2016 riportano, nell’ambito delle possibilità di scelta di ogni singola stazione appaltante, due possibilità alternative:

1. la prima basata sull’attribuzione discrezionale di un coefficiente variabile tra zero e uno, da parte di ciascun commissario di gara; (da moltiplicare poi per il punteggio massimo attribuibile in relazione al criterio),
2. la seconda basata sul confronto a coppie tra le offerte presentate, da parte di ciascun commissario di gara, in modo da attribuire, anche in questo caso, un coefficiente variabile tra zero ed uno, che sarà poi moltiplicato per il punteggio massimo attribuibile relazionato al singolo criterio oggetto di giudizio.

Quest’ultima possibilità viene prevista allo scopo di ridurre il numero di valutazioni discrezionali e le relative motivazioni da assegnare da parte dei singoli commissari.

Il metodo del confronto a coppie, che definiremo semplice, ossia con il solo impiego di una matrice triangolare alta, presenta tuttavia il rischio di creare inconsistenza nei giudizi, stante la possibile violazione della c.d. "proprietà transitiva".

Per tale ragione le le linee guida ANAC suggeriscono l’impiego della metodologia AHP come sopradescritta, proprio per valutare la coerenza e la transitività dei giudizi espressi, risultando perciò così di gran lunga preferibile al metodo che abbiamo definito del semplice confronto a coppie o con matrice triangolare.

Pertanto, in una gara dove vi sono numerose offerte e dove sussite il rischio di avere inconsistenza dei giudizi, il metodo AHP appare assolutamente il più idoneo ed adatto allo scopo, dando luogo alla formazione dei coefficienti variabili fra zero ed uno che saranno poi moltiplicati per il punteggio massimo (peso o subpeso) attribuito al criterio o sub-criterio della gara in questione.

Per ricorrere al metodo AHP e alla sua applicazione, si fa riferimento ad una metodologia semplificata, al fine di ridurre la complessità computazionale legata al calcolo dell’autovalore principale e del relativo autovettore normalizzato, ed in particolare alla metodologia descritta innanzi nella sezione relativa alle metodologie approssimate del metodo AHP.

Tale metodologia è illustrata nello specifico anche nei quaderni AVCP del Dicembre 2011 avente ad oggetto “IL CRITERIO DI AGGIUDICAZIONE DELL’OFFERTA ECONOMICAMENTE PIÙ VANTAGGIOSA”.

Tale metodologia può venire applicata anche ipotizzando l’impiego di un normale foglio di calcolo elettronico, tipico di programmi su licenza come Excel o software open-source come Open office o Libre office, secondo l’esempio sotto mostrato, tipico di una gara dove sono presenti sei concorrenti o offerte.

Il foglio elettronico contiene, nella porzione di sinistra, la matrice utilizzata per l’inserimento dei giudizi da parte dei commissari, mentre nella porzione di destra sono eseguiti i calcoli relativi alla determinazione dell’autovettore (Xi), dell’autovettore normalizzato (Pi), dell’autovalore principale, il cui valore è evidenziato in basso a destra nella cella colorata di arancione sotto la scritta λ_max.

In basso si trovano le celle per il calcolo dei coefficienti CI, RI (quest’ultimo ricavabile dai valori indicati in letteratura e pertanto standardizzato) e CR, essenziale per determinare la validità o meno dei giudizi espressi come si vede in Figura 5.

Nel riquadro di sinistra è posta la matrice dei confronti a coppie, dove i commissari andranno ad inserire i giudizi di preferenza per il singolo confronto fra i concorrenti, qui denominati A, B, C, D, E ed F.

L’inserimento dei valori avviene nel modo seguente: sulla diagonale principale della matrice, quella evidenziata dalle celle colorate di giallo, sarà inserito il valore 1, poiché ogni singolo elemento confrontato con sé

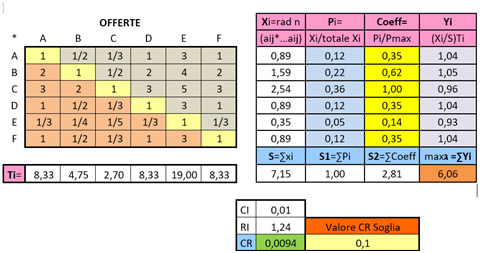
Figura 5: Confronto a coppie AHP

stesso può produrre solo parità secondo la scala se mantica di Saaty e quindi il relativo indice numerico di giudizio è 1.

Si procede così con la valutazione dei concorrenti per righe, iniziando quindi dal concorrente A.

Se il concorrente per riga è preferito rispetto a quel lo della colonna con cui si confronta (ad esempio A è preferito rispetto a B), allora si inserisce nella cella corrispondente il valore che secondo la scala di Saaty corrisponde al grado di preferenza espresso dal commissario (Il valore sarà inserito nelle celle colorate di marrone, poste nella porzione triangolare alta della matrice, come nei confronti a coppie usuali).

Se il concorrente per riga è considerato meno preferito rispetto al corrispondente in colonna, allora il valore numerico della scala di Saaty con cui si esprime la preferenza di quest’ultimo, sarà inserito nella corrispondente cella che incrocia i due concorrenti nella porzione triangolare bassa della matrice (quella evidenziata in colore arancione) oppure si può inserire nella porzione triangolare alta della matrice (quella colorata di marrone) i corrispondenti reciproci esprimenti il grado di giudizio sempre secondo la scala di Saaty esaminata in precedenza.

I valori uguali a 1 sulle celle diverse dalla diagonale superiore della matrice, indicano parità di giudizio (nella matrice in esame B e C sono stati preferiti ad A, che a sua volta è stato preferito a D, E ed F).

La porzione a destra del foglio elettronico, contiene i dati per la valutazione dell’autovettore normalizzato ottenuto moltiplicando gli elementi di ogni riga del la matrice iniziale, ed estraendone la radice n-esima del risultato ricavato, dove n è il rango della matrice (in questo caso n=6) per ricavare i valori delle singole componenti (celle colore bianco sotto la sigla X_i) dell’autovettore della matrice, e normalizzandolo attraverso la divisione successiva per il totale della somma delle componenti dell’autovettore testé ricavato, al fine di calcolare l’autovettore normalizzato (celle colore celeste scuro sotto la sigla Pi).

L’autovalore principale è calcolato moltiplicando ogni elemento dell’autovettore normalizzato per il reciproco del numero risultante dalla somma delle componenti dell’autovettore non normalizzato e per la somma delle colonne della matrice non normalizzata, i cui valori sono posti qui a fianco della sigla T_i e sommandone infine i risultati così ottenuti per dare λ_max (indicato nella cella color arancione scuro posta sotto la cella “maxλ =∑Yi”.

La consistenza è valutata usando sempre l’indice di consistenza così come nel metodo canonico.

In questo caso, abbiamo un valore di CR ampiamente sotto 0,1 (valore soglia) come evidenziato nella cella color verde accanto alla sigla CR che mostra come i risultati posti nella matrice sono consistenti fra loro. Questi risultati sono considerabili accettabili e pertanto si possono utilizzare i pesi derivanti dall’autovettore normalizzato e procedere al calcolo dei coefficienti relativi al criterio o subcriterio oggetto di esame che saranno utilizzati successivamente nello svolgimento della gara. (in questo caso sono i valori evidenziati in giallo nelle celle di destra sotto la sigla Coeff)

Nella Figura 6 immagine vediamo un esempio di confronto non consistente, ossia che presenta un CR maggiore della soglia, come evidenziato in rosso nella cella corrispondente al valore calcolato.

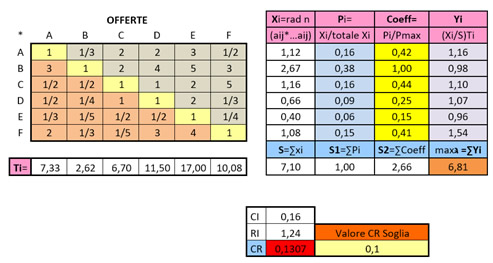
Figura 6: Esempio di confronto

In questo caso, il commissario dovrà rivedere i suoi giudizi fino a quando il valore di CR sarà inferiore al valore soglia di 0,1 per ottenere così consistenza degli stessi. Chiaramente la matrice può essere personalizzata in diversi modi.

Nell’ultimo caso Figura 7 vediamo una matrice che riporta i giudizi di cui all’esempio soprastante di matrice consistente ma in cui le celle sono colorate in modo diverso per evidenziare la tipologia dei giudizi, ossia in celeste, quando leggendo le offerte per riga le stesse sono preferite a quelle della colonna corrispondente, ed in arancione, se le offerte per riga sono considerate inferiori. In bianco abbiamo giudizi di parità.

In giallo nella Figura 7 è evidenziata sempre la diagonale principale.

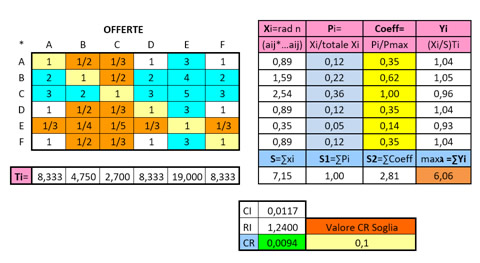
Figura 7: Diagonale Principale

Considerazioni finali sul metodo AHP nella valutazione degli elementi qualitativi negli appalti pubblici

Il metodo AHP si rivela di estrema utilità nel caso della valutazione degli elementi qualitativi negli appalti pubblici in quanto consente di verificare se i giudizi soddisfano alla condizione di transitività degli stessi, ossia se presentano concordanze di giudizio idonee a indirizzarle in una direzione concorde nella scelta del concorrente migliore.

La possibilità di verificare la transitività dei giudizi grazie al CR (Consistency Ratio) calcolabile con tale metodologia è un indice di affidabilità degli stessi al contrario di ciò che accadrebbe con un metodo di confronto a coppie eseguito con l’impiego della sola matrice triangolare alta.

Il metodo AHP si rivela quindi più affidabile e quindi ne è estremamente consigliato il suo uso ed il suo impiego nella scelta dell’offerente migliore, ossia di colui che presenta caratteristiche tecniche reputate idonee per lo svolgimento della prestazione in oggetto.

Di contro, il metodo AHP trova difficoltà di applicazione per le procedure di gara dove sono presenti più di 15 concorrenti, sia per la difficoltà di implementazione della matrice, sia per l’oggettiva difficoltà di avere i parametri di riferimento per la verifica del CR (Consistency Ratio), mancando parametri facilmente reperibili in letteratura.

Per gare con più di 15 concorrenti occorre dunque valutare con attenzione la sua applicazione, ricorrendo eventualmente a soluzioni che ne consentano un uso con implementazioni in grado di evitare inconsistenza tra i vari giudizi.

Pertanto, se ne conclude che, in una gara con meno di sedici concorrenti, anche al fine di ridurre il numero di valutazioni discrezionali e le relative motivazioni, la metodologia AHP appare quella più affidabile per verificare la corretta espressione dei giudizi, potendo garantire il soddisfacimento della proprietà transitiva relativa agli stessi, come d’altronde suggerito nelle linee guida dell’ANAC n° 2/2016 e qui ampiamente dimostrato.

A cura di Ing. Fabio Talini
Funzionario presso il Comune di San Miniato
Avv. Francesco Barchielli
Direttore di www.urbanisticaitaliana.it
Direttore di www.appaltieriserve.it
Avvocato Amministrativista in Firenze: www.studiobarchielli.it